Game of Life

Einführung:

Zur Wiederholung der beiden Schuljahre und zum Warmwerden haben wir uns mit dem Game of Life beschäftigt. Dabei handelt es sich um ein von dem englischen Mathematiker John Horton Conway entworfenes System, bei welchem Zellen simuliert werden, die durch bestimmte Regeln sterben oder geboren werden. Um die verschiedenen Regeln besser zu verstehen, betrachten wir nun folgendes Beispiel:

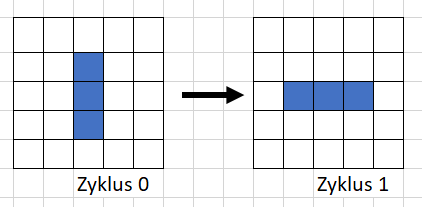
Wir haben nun zwei Felder, die jeweils unterschiedliche Fortschritte in einem Prozess zeigen. Diese Fortschritte sind die sogenannten Zyklen, die bei 0 anfangen und unendlich weit gehen können. In der obigen Grafik fangen wir mit dem nullten Zyklus an. Bei diesem und auch allen anderen stellen die weißen Quadrate tote und die blauen Quadrate lebende Zellen dar. Um zu wissen, wie man von dem nullten zum ersten Zyklus kommt, muss man erst die Regeln kennen lernen, die bestimmen ob eine Zelle im nächsten Zyklus lebt oder tot ist.

Regeln:

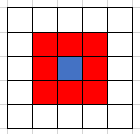
Bei den Regeln wird jede Zelle (blau) einzeln betrachtet. Über ihren Zustand im nächsten Zyklus bestimmen die 8 Felder (rot), die direkt um diese herum angesiedelt sind.

1.: Geburt einer Zelle:

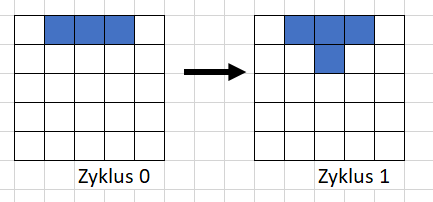
Eine Zelle wird dann Geboren, wenn sie exakt 3 lebende Nachbarn hat.

2.: Überleben einer Zelle:

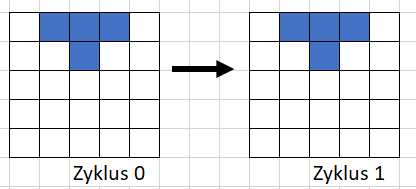
Eine lebende Zelle bleibt dann im nächsten Zyklus bestehen, wenn sie 2 oder 3 lebende Nachbarn hat.

3.: Vereinsamung einer Zelle:

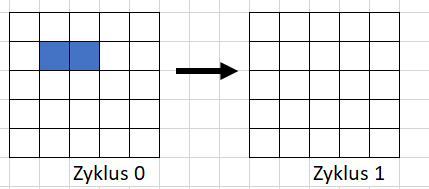
Eine Zelle vereinsamt und stirbt damit ab, wenn sie weniger als 2 direkte Nachbarn hat.

4.: Überbevölkerung:

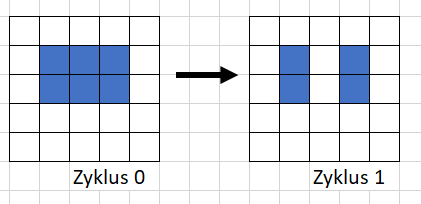
Sollte eine Zelle mehr als 3 Nachbarn haben, so stirbt sie ebenfalls ab.

Implementierung:

Für die Implementierung haben wir von Herrn Reichelt ein vorgefertigtes Raster bekommen, welches man in der unteren Abbildung sehen kann.

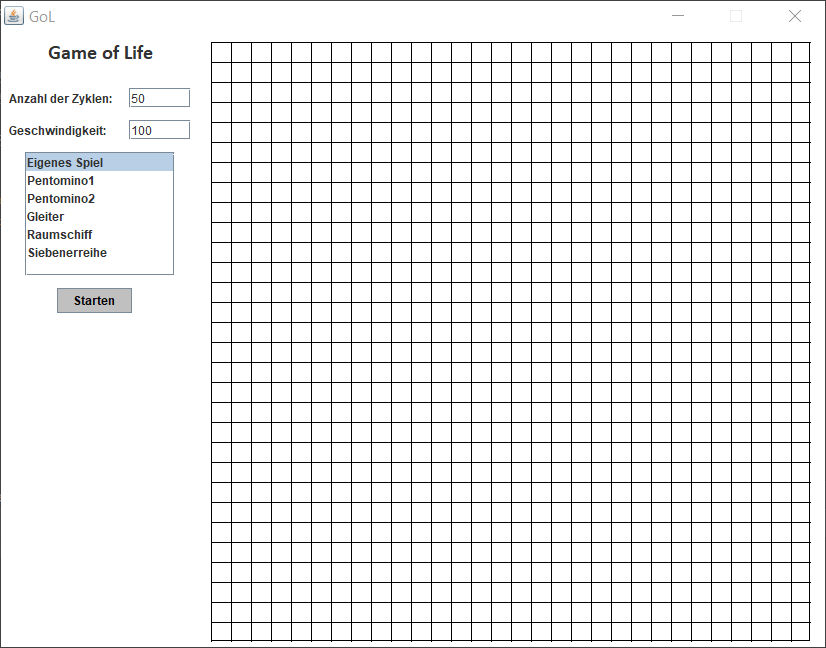
In dieses Raster mussten dann noch zwei Methoden eingefügt werden:

private int anzahlLebender(int i, int j) {
    //zaehlt Anzahl der lebenden Nachbarn
    //ergaenzen
    int anzahl = 0;
    
    for (int row = i - 1; (row <= i + 1) && (row < N); row++) {
        for (int column = j - 1; (column <= j + 1) && (column < N); column++) {
            if (zustand[row][column] == lebend) {
                anzahl++;
            }
        }
    }
    if (zustand[i][j] == lebend) {
        anzahl--;
    }
    return anzahl;
} // Ende AnzahlLebender

Um in der zweiten Methode, die überprüft, ob eine Zelle stirbt oder nicht, die Anzahl der Nachbarn zu bestimmen, kann man die oben abgebildete Methode benutzen. Dabei werden der Methode die Position der Zelle, deren Nachbarn überprüft werden sollen, als Parameter übergeben. Sie werden hier als i und j bezeichnet. Zwar ist es egal, welche der beiden man als Reihe und welchen der beiden als Spalte definiert, ich haben aber in meiner Lösung immer zuerst die Reihe ( hier als “row”) und j dann als Spalte (“column”) definiert.

Die Variable anzahl beschreibt dabei den Rückgabewert. Also die Anzahl der lebenden Nachbarn. Sie wird mit 0 initialisiert, da es noch keine erkannten Nachbarn gibt.

Um alle neun Felder (die eigentliche Zelle wird mit überprüft) auf ihren Zustand zu testen, werden zwei for-Schleifen verwendet. Die erste der beiden geht durch die verschiedenen Reihen durch, wobei sie eine Reihe oberhalb der eigentlichen Zelle anfängt und eine Reihe unterhalb der Zelle aufhört. Das Gleiche Prinzip wendet die for-Schleife an, die in die erste eingebunden ist: Für jede Reihe (also für jeden Durchlauf der ersten for-Schleife) geht sie durch die drei Spalten. Dabei ist es aber bei beiden Schleifen wichtig, eine NullPointerException zu vermeiden, indem man den Bereich abgrenzt. Dies geschieht durch die Länge des Feldes (dargestellt durch N). Für jedes der neun Felder wird dann mit einer Verzweigung der Zustand überprüft.

Zum Schluss muss dann noch überprüft werden, ob die Zelle in der Mitte am Leben ist. Sollte dies der Fall sein, so wird anzahl dekrementiert, da wir diese Zelle nicht mitzählen wollen.

public Gitter uebergang(Graphics g) {
    int[][] zustandNeu = new int[N][N];
    //Hier ergaenzen
    for (int row = 1; row < N - 1; row++) {   //Zeile
        for (int column = 1; column < N - 1; column++) {       //Spalte
            if(zustand(row,column) == lebend){   
                if(anzahlLebender(row,column) == 2 || anzahlLebender(row,column) == 3){
                   zustandNeu[row][column] = lebend;  //Bei 2 oder drei Nachbarn überlebt eine Zelle
               }else {
                   zustandNeu[row][column]=tot;
               } 
                                                      //Sonst ist sie tot
            }else if(zustand(row,column)==tot ){      //sollte die Zelle schon tot sein,
               if(anzahlLebender(row,column)==3){     //muss nur noch überprüft werden, ob sie geboren wird.
                   zustandNeu[row][column] = lebend;
               }else{
                       zustandNeu[row][column]=tot;
                }
            }
        }
    }
    return new Gitter(g, zustandNeu);
} // Ende uebergang

Die Methode uebergang überprüft für jede Zelle, ob sie im nächsten Zyklus tot oder lebendig ist. Dafür muss zuerst ein neues Array erzeugt werden, dass den Zustand der Zellen speichert. Auch hier werden wieder zwei for-Schleifen angewandt, die aber im Gegensatz zu der ersten Methode das komplette Spielfeld abdecken. Ich habe dabei die Überprüfung für eine lebende und eine tot Zelle aufgeteilt. Bei der lebenden muss nur überprüft werden, ob sie zwei oder drei Nachbarn haben. Damit sie auch im nächsten Zyklus leben bleiben. In allen anderen Fällen stirbt die Zelle.

Sollte der Zustand der Zelle tot sein, so muss nur überprüft werden, ob sie geboren wird, denn sonst bleibt sie tot.