Graphen sind Teil der Graphentheorie und dienen als Datenstruktur zur Speicherung von Beziehungen zwischen Objekten.
allgemeine Definition
Graphen bestehen aus Knoten und Kanten. Dabei verbinden die Kanten einen Knoten mit einem anderem. Jeder Knoten kann eine beliebige Anzahl an Kanten haben, mit welchen er verbunden ist.
Das Königsberger Brückproblem
Eines der ersten Probleme im Hinblick auf Graphen stellt das Königsberger Brückenproblem dar. Dieses wurde von Leonard Euler aufgestellt und beschäftigt sich mit der Frage, ob man alle Brücken in der Stadt Königsberg in einer Tour überqueren kann, ohne dabei eine Brücke zwei mal zu überqueren.

In der obigen Karte sind die Brücken mit Grün kenntlich gemacht. Um nun das Problem in einem Graphen zu veranschaulichen, werden die verschiedenen Stadtteile als Knoten, und die Brücken als Kanten definiert.
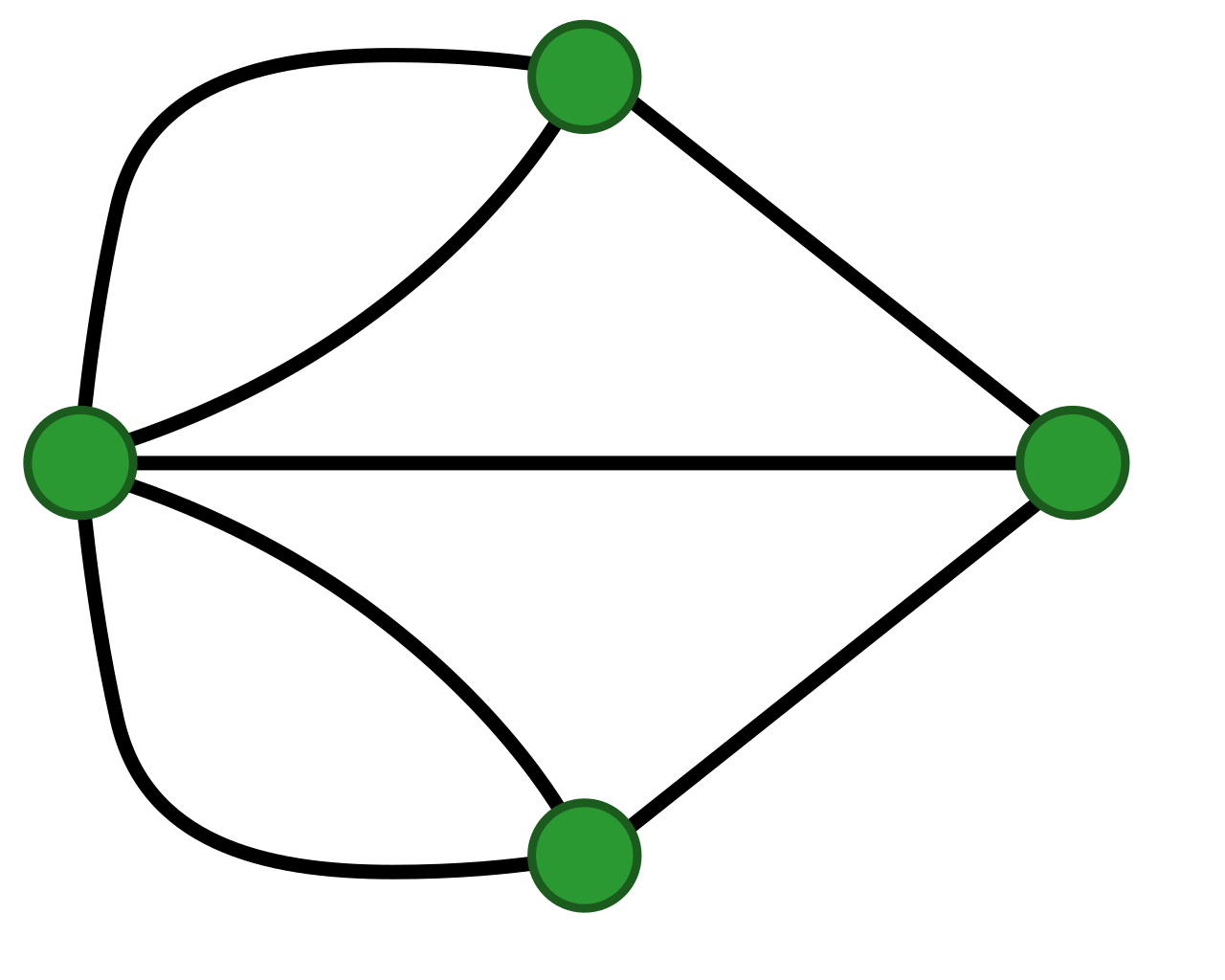
Es stellt sich raus das es keine sogenannte Euler-Tour gibt, welche das vorhin genannte Kriterium erfüllt. Dies hängt mit dem Grad der Knoten zusammen. Also der Anzahl an Kanten, mit denen ein Knoten immer verbunden ist.
Dabei gilt: Eine Euler-Tour ist dann möglich, wenn jeder Knoten in dem Graph eine gerade Anzahl an Kanten hat. Jeder Grad also gerade ist.
Hamiltonkreisproblem
Das Hamiltonkreisproblem beruht auf dem von Sir William Rowan Hamilton erfundenen Brettspiel „Traveller’s Dodecahedron or A Voyage Round The World“.
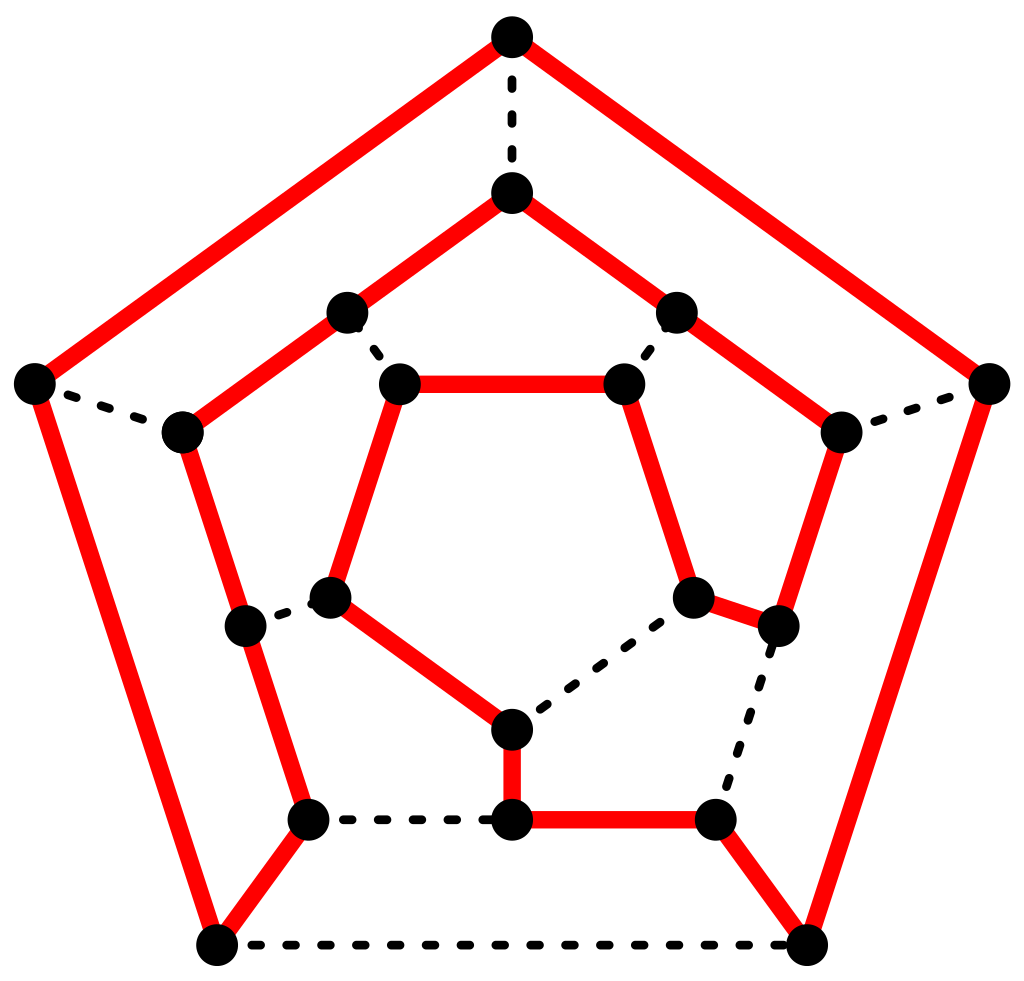
Bei dem Hamiltonproblem geht es darum, einen Weg über alle Knoten in dem Graph zu finden. Dabei darf allerdings nur jeder Knoten nur einmal in dem Weg vorkommen. Außerdem muss der Weg dort aufhören, wo er auch angefangen hat. Eine mögliche Lösung für das Problem ist ebenfalls im obigen Bild dargestellt.
Im Gegensatz um Königsberger Brückenproblem sind bei diesem Problem die Knoten im Fokus. Außerdem gehört das Hamiltonkreisproblem zur Klasse der NP-Probleme (Probleme, welche sich nur in nicht-polynomialer Zeit lösen lassen). Damit ist es ein Problem, welches sich nur sehr schwer lösen lässt.
Umsetzung
Grundsätzlich gibt es zwei Möglichkeiten, einen Graphen zu speichern:
1. Adjazenzliste
Eine solche Liste wird durch die List-Datenstruktur realisiert. Dabei wird in eine Liste jeder Knoten gespeichert. Für jeden Knoten wird dann in einer weiteren Liste gespeichert, mit welchen Knoten er verbunden ist.

Die obige Liste ist folgendem Graphen zuzuordnen:

Dieser Graph ist ungerichtet, da man erkennen kann, dass bei zwei Verbunden Knoten beide Knoten ihre Verbindung zum jeweiligen anderen speichern:
a -> e
e -> a
2. Adjazenzmatrix
Die Adjazenzmatrix speichert einen Graphen in Form eines zweidimensionalen Arrays.

Die obige Matrix resultiert in folgendem Graph:
Dabei hat jeder Knoten jeweils eine Spalte und Zeile. Eine Verbindung zwischen zwei Knoten ensteht dadurch, dass in der Spalte des Knoten 1 und in der Zeile von Knoten 2 eine 1 steht. Ist dort eine 0 vorhanden, so verbindet keine Kante diese beiden Knoten. Sollte eine Gewichtung der Kanten vorliegen, so werden die Zahlen in der Matrix durch die entsprechenden Gewichtungen ersetzt. Sollte dann keine Verbindung vorhanden sein, so bleibt das entsprechende Kästchen leer.
Vor- und Nachteile
Der auffälligste Unterschied zwischen Matrix und Liste ist, dass bei einer Matrix durch das zweidimensionale Array keine Möglichkeit besteht, effektiv einen neuen Knoten einzufügen. Allerdings muss auch bedacht werden, dass eine Liste immer komplett durchlaufen werden muss, um zu überprüfen, ob eine Kante vorhanden ist. Dadurch ergibt sich:
Eine Adjazenzliste sollte bei einem Graphen mit vielen Schreiboperationen gewählt werden, während eine Ajdazenzmatrix bei schnellen Leseoperationen gewählt werden sollte.
Formale Definition
Ähnlich wie bei Automaten kann auch ein Graph durch eine formale Definition beschrieben werden. Dabei werden die Kanten als Verbindungen zwischen zwei Knoten angegeben:
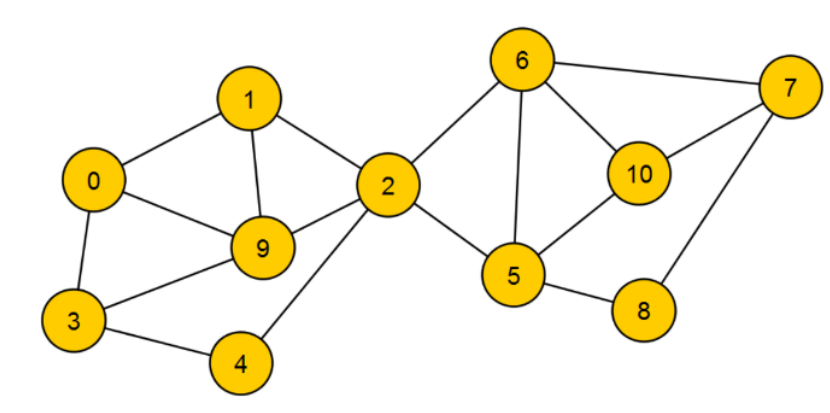
Für den obigen Graph ergibt sich also folgende Definition:
ist die Menge aus Knoten:
ist die Menge aus Kanten und wird zweidimensional angegeben. Jede Kante ist dabei eine Menge aus Anfangs- und Endknoten.
Der Grad eines Knoten wird mit angegeben: bedeutet, dass der Knoten 1 einen Grad von 3 besitzt. Die maximale Anzahl an Kanten eines Knoten in einem ungerichteten Graphen wird durch die Gleichung beschrieben. Dabei ist die maximale Anzahl an Kanten, und die Anzahl an Knoten in dem Graph.
Wenn zwei Knoten miteinander verbunden sind, so werden sie als adjazent bezeichnet. Das Gegenteil dazu heißt inzident.
Kombinationen aus Kanten oder Knoten werden wie folgt beschrieben:
- eine Kantenfolge ist ein Weg über Kanten, bei dem Kanten auch mehrfach vorkommen können.
- ein Kantenzug ist eine Kantenfolge ohne Wiederholungen.
- ein Weg ist ein Kantenzug ohne Wiederholungen von Knoten.
- ein Kreis ist ein abgschlossener Weg.
Ein Graph wird dabei als zusammenhängend bezeichnet, wenn jeder Knoten von jedem anderem Knoten erreicht werden kann.
Implementierung
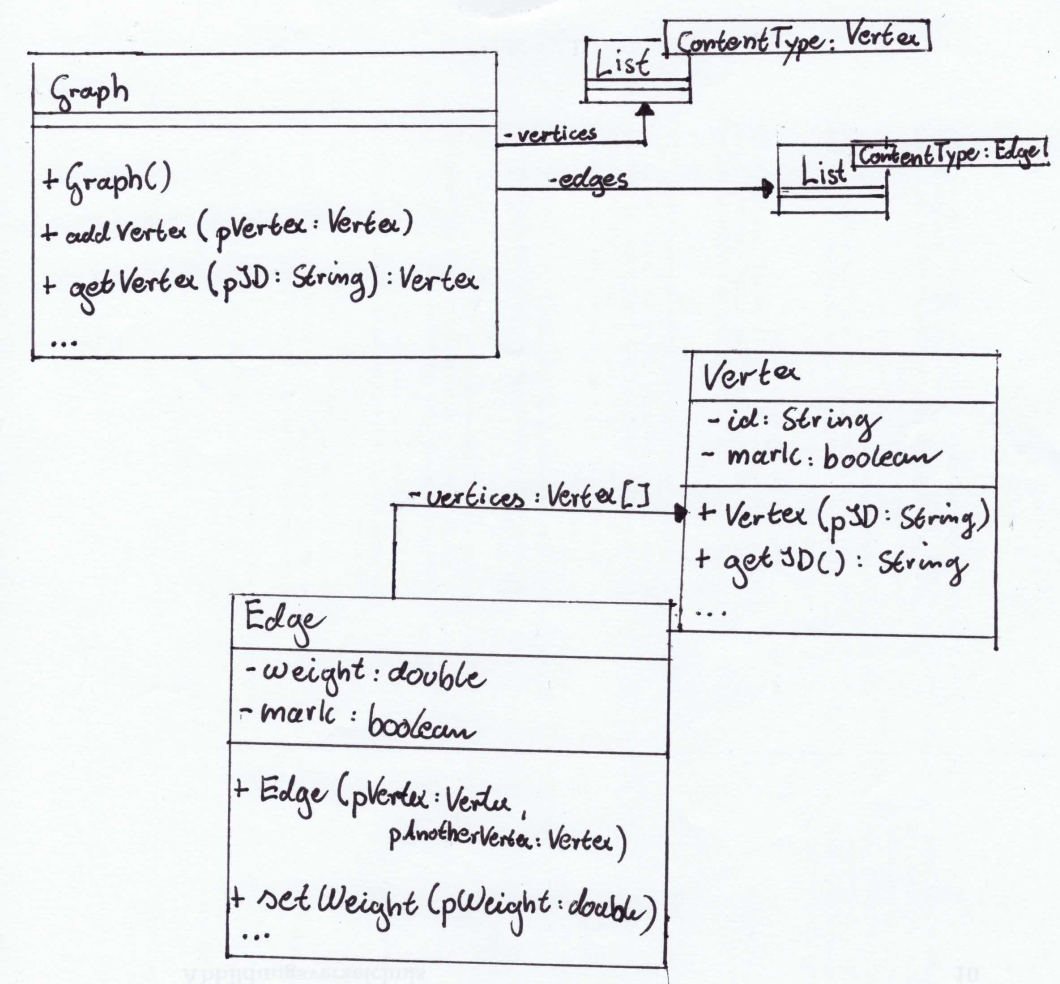
Eine Implementierung stellt das Land NRW bereit. Dabei werden der Graph, sowie die Knoten und Kanten jeweils als Objekt dargestellt. Im folgenden werden die Implementierung in einem Implementationsdiagramm visualisiert.
Graphen durchsuchen
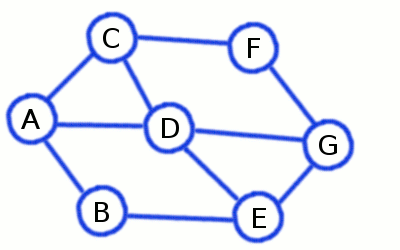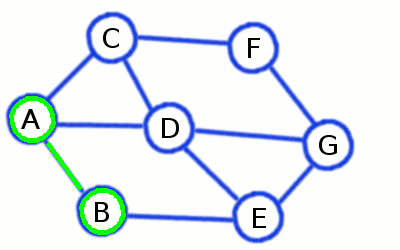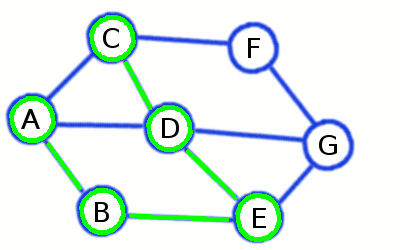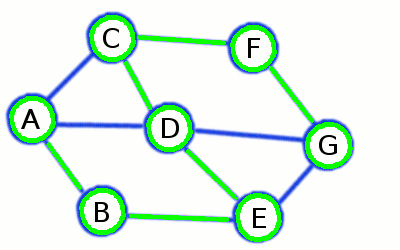
Ähnlich wie bei den Binärbäumen, gibt es auch bei einem Graphen Möglichkeiten diesen zu durchsuchen. Dabei wird ein Startknoten festgelegt, bei dem die Suche beginnt. Im folgenden werden die Algorithmen für das komplett Dursuchen eines Graphen vorgestellt. Sie könnten aber sehr leicht so abgewandelt werden, dass überprüft wird, ob ein Weg von einem Knoten zu einem anderen besteht.
Breitendurchlauf
Bei dem Breitendurchlauf werden erste alle Nachbarknoten des aktuellen Knoten gespeichert. Für jeden dieser Knoten werden dann wieder alle Nachbarknoten gespeichert.
Pseudocode
MARKIERE Startknoten v
FÜGE v in eine Schlange D EIN
SOLANGE D nicht leer:
NEHME einen Knoten w aus D
LÖSCHE w aus D
FÜR jeden mit w verbundenen Knoten u:
WENN u nicht markiert:
MARKIERE u
FÜGE u in D EIN

Implementierung
Für die Implementierung werden die Klassen des Ministeriums verwendet. Neben der Graph,Vertex und Edge Klasse wird auch die Klasse Queue benötigt, da sie die Schlange D aus dem Pseudocode repräsentiert.
public String breadthSearch(Graph graph, String start) {
graph.setAllVertexMarks(false);
String result = "";
Queue<Vertex> d = new Queue<>();
Vertex startVertex = graph.getVertex(start);
if (startVertex == null) {
return "ERROR: Wrong start vertex.";
}
startVertex.setMark(true);
d.enqueue(startVertex);
while (!d.isEmpty()) {
Vertex current = d.front();
result += " " + current.getID();
d.dequeue();
List<Vertex> neighbors = graph.getNeighbours(current);
for (neighbors.toFirst(); neighbors.hasAccess(); neighbors.next()) {
Vertex neighbor = neighbors.getContent();
if (!neighbor.isMarked()) {
neighbor.setMark(true);
d.enqueue(neighbor);
}
}
}
return result;
}
Tiefendurchlauf
Beim Tiefendurchlauf wird ein Pfad solange entlangegangen, bis ein Knoten erreicht wird, der keine weiteren noch nicht besichtigen Nachbarknoten hat. In diesem Fall geht man einen Knoten zurück, und geht einen anderen Pfad entlang, bis alle erreichbaren Knoten markiert wurden.
Pseudocode
MARKIERE Startknoten v
FÜGE v in eine Stapel D EIN
SOLANGE D nicht leer:
NEHME einen Knoten w aus D
LÖSCHE w aus D
FÜR jeden mit w verbundenen Knoten u:
WENN u nicht markiert:
MARKIERE u
FÜGE u zu D hinzu
Implementierung
Bei der Implementierung wird auch die Klasse Stack für den Stapel D benötigt.
public String depthSearch(Graph graph, String start) {
graph.setAllVertexMarks(false);
String result = "";
Stack<Vertex> d = new Stack<>();
Vertex startVertex = graph.getVertex(start);
if (startVertex == null) {
return "ERROR: Wrong start vertex.";
}
startVertex.setMark(true);
d.push(startVertex);
while (!d.isEmpty()) {
Vertex current = d.top();
List<Vertex> neighbors = graph.getNeighbours(current);
for (neighbors.toFirst(); neighbors.hasAccess(); neighbors.next()) {
Vertex neighbor = neighbors.getContent();
if (neighbor.isMarked()) continue;
neighbor.setMark(true);
d.push(neighbor);
}
// dem Stack wurde nichts hinzugefügt. Daher hat der aktuelle Knoten keine Nachbarn
if (d.top().getID().equals(current.getID())) {
result += " " + current.getID();
d.pop();
}
}
return result;
}