Bisher hatten wir Automaten mit einer endlichen Menge an Zuständen. Was passiert aber, wenn man einen Automaten bauen soll, dessen formale Sprache folgendermaßen aufgebaut ist:

Der Automat $A$ akzeptiert nur Eingaben, bei denen es genauso viele a´s wie b´s gibt. Allerdings ist die Anzahl der beiden Zeichen nicht beschränkt. Daher bräuchte man einen Automaten, der unendlich viele Zustände abbilden kann.

Der Kellerspeicher

Um solche Eingaben ebenfalls durch einen Automaten darstellen zu können, wird ein Speicher, der sogenannte Keller eingeführt. Das Verhalten des Kellers ist ähnlich zu dem der Datenstruktur Stack:

• Es kann immer nur das oberste Objekt gelesen/gelöscht werden.
• Fügt man ein neues Objekt hinzu, wird dieses oben eingefügt.

Um den Kellerspeicher auf die obige Sprache anzuwenden, muss zuerst geschaut werden, wie viele a´s dort enthalten sind. Dafür wird für jedes a ein Symbol in den Stapel des Kellerspeichers eingefügt. In unserem Fall ist das Symbole ein A. Dannach wird für jedes b ein A wieder vom Stapel entfernt. Es gibt nun drei mögliche Ausgänge:

1. Der Stapel ist nicht leer → Es sind weniger a´s als b´s in der Eingabemenge.
2. Der Stapel ist leer, es gibt aber noch Zeichen in der Eingabe → Es sind mehr a´s als b´s.
3. Die Eingabemenge wurde komplett gelesen, und der Stapel ist leer → Die Eingabe ist gültig.

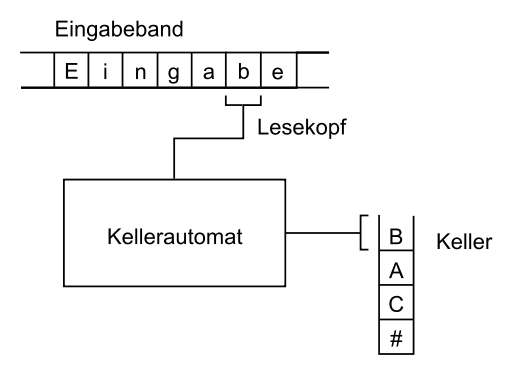Beispiel für einen Kellerautomat mit Kellerspeicher, Quelle: Wikipedia

Regeln

Beim Einlesen des Kellerspeichers existieren bestimmte Regeln:

1. Wird das oberste Zeichen eines Kerllerspeichers gelesen, so wird es automatisch gelöscht.
2. Das unterste Zeichen eines Speichers stellt immer ein # dar. Auch wenn dieses Kelleranfangssymbol gelesen wird, wird es gelöscht!
3. $\varepsilon$ stellt ein leeres Symbol dar, welches dem Stapel hinzugefügt werden kann.

Übergangsgraph

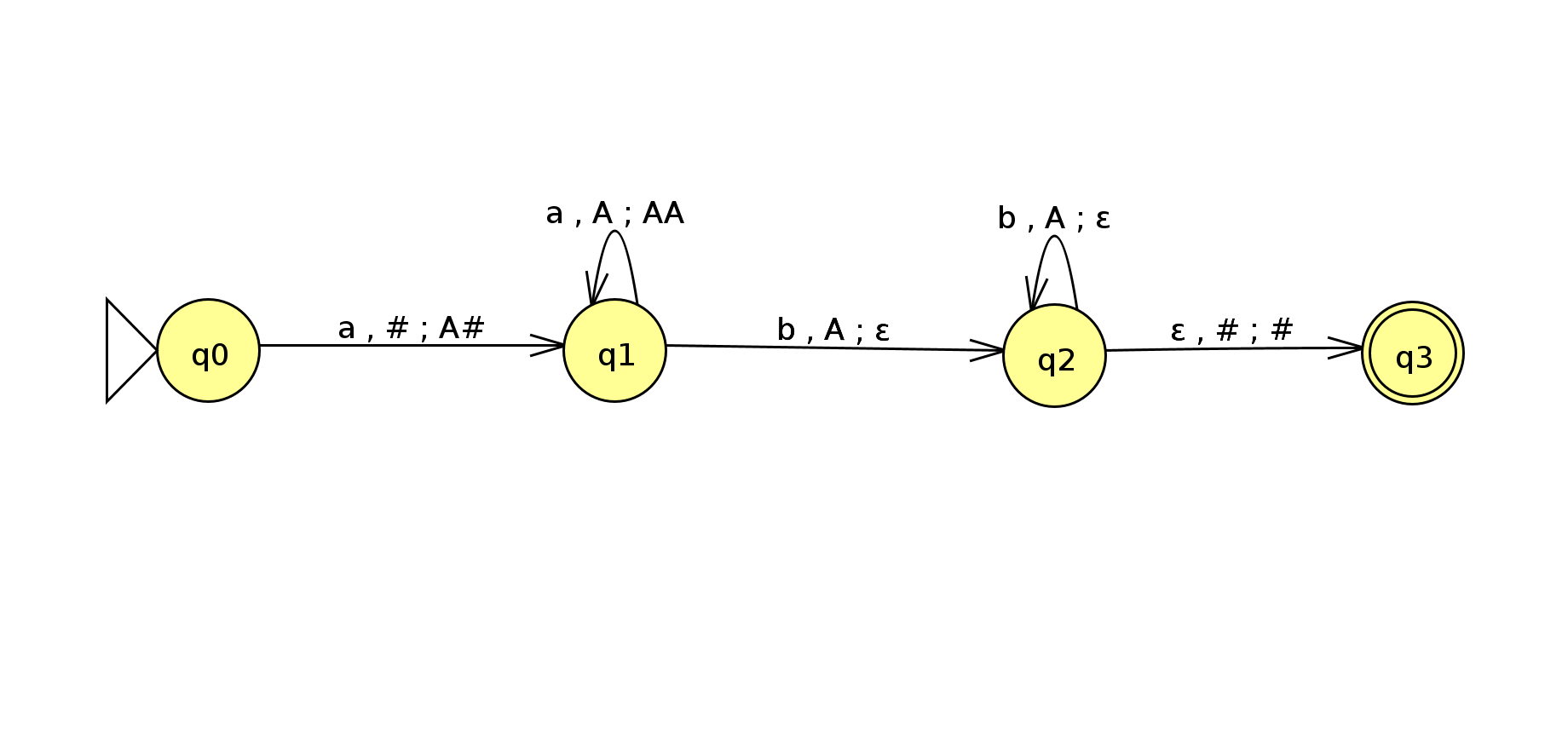
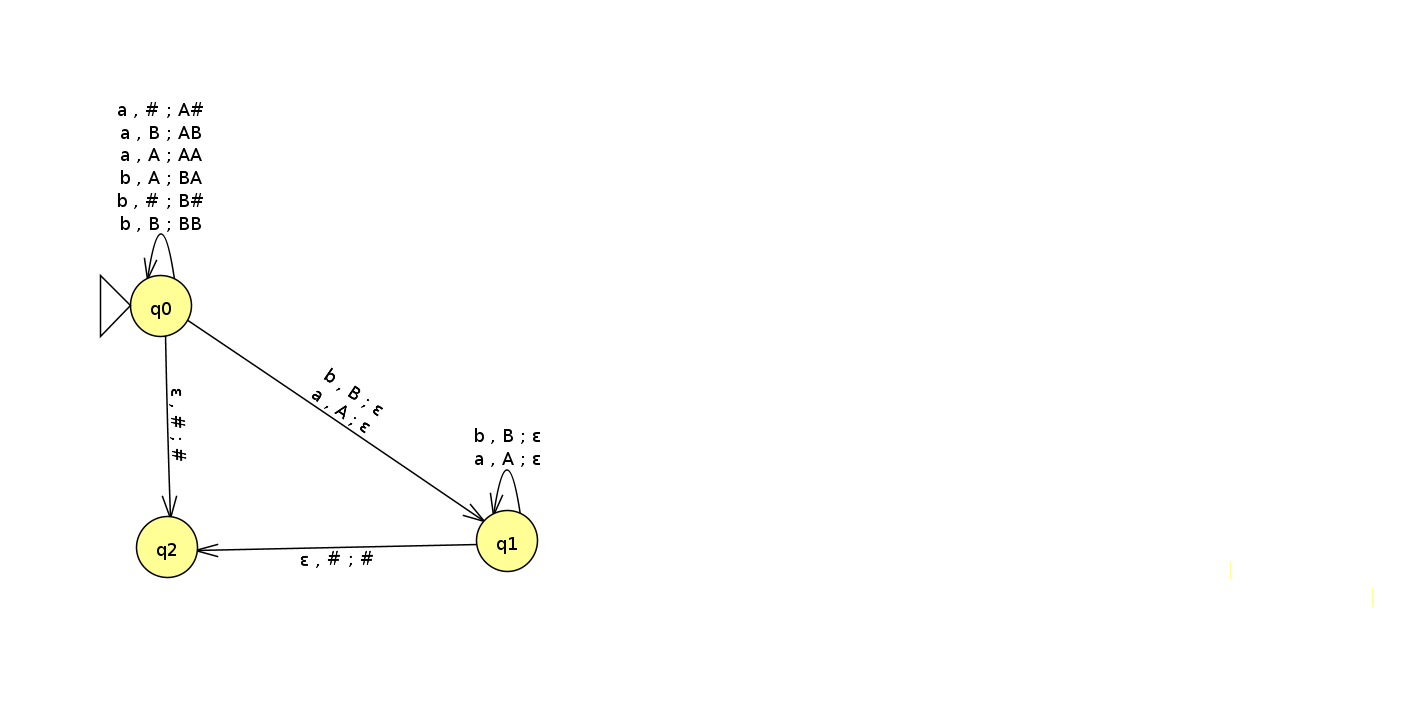
Die Übergänge sind dabei als Verzweigungen zu verstehen: Wenn a das aktuelle Zeichen aus der Eingabemenge ist, und # im Kellerspeicher liegt, füge erste # und dann A zum Speicher hinzu. (Aus dem Übergang von q0 zu q1.)

Sollten mehrere Zeichen gleichzeitig in den Speicher eingefügt werden, so wird die Zeichenkette von rechts nach links in den Automat eingefügt.

Der letzte Übergang von q2 nach q3 dient dazu, dass überprüft wird, ob der Speicher und die Eingabe jeweils leer sind.

Definition eines Kellerautomaten

Neben den Bekannten Bestandteilen bei der Definition eines normalen Automaten, ergeben sich beim Kellerautomaten einige weiter Bestandteile.

• $\Gamma$ bezeichnet das Kelleralphabet. Also alle Zeichen, die der Kellerspeicher beinhalten kann.
• $k_0$ ist das Kelleranfangssymbol. In unserem Fall ist das #.

Implementierung

Im folgenden wird die Implementierung für einen Kellerautomat dargstellt, bei dem getestet wird, ob ein Wort umgekehrt wurde. Dabei wird das Ursprungswort und das umgedrehte Wort durch eine 0 getrennt. Der Kellerspeicher wird dabei mit einem Stack realisiert.

public class PalindromAutomat {
    private Stack<Character> kellah = new Stack<Character>();

    public boolean pruefe(String pWort) {
        int z = 0;
        pWort += " ";
        kellah.push('#');

        for (int i = 0; i < pWort.length(); i++) {
            char l = pWort.charAt(i);

            switch(z) {
                case 0:
                    if (l == 'a') {
                        char kL = readTopLetter();
                        if (kL == 'A') {
                            insertCharacter('A');
                            insertCharacter('A');
                        }else if (kL == '#') {
                            insertCharacter('#');
                            insertCharacter('A');
                        }else if (kL == 'B') {
                            insertCharacter('B');
                            insertCharacter('A');
                        }else {
                            return false;
                        }

                        z = 0;
                    }else if (l == 'b') {
                        char kL = readTopLetter();
                        if (kL == 'A') {
                            insertCharacter('A');
                            insertCharacter('B');
                        }else if (kL == '#') {
                            insertCharacter('#');
                            insertCharacter('B');
                        }else if (kL == 'B') {
                            insertCharacter('B');
                            insertCharacter('B');
                        }else {
                            return false;
                        }
                        z = 0;
                    }else if (l == '0') {
                        z = 1;
                    }else {
                        return false;
                    }
                    break;
                case 1:
                    char kL = readTopLetter();
                    if (l == 'b' && kL == 'B') {
                        z = 1;
                    }else if (l == 'a' && kL == 'A') {
                        z = 1;
                    }else if (l == ' ' && kL == '#') {
                        z = 2;
                    }else {
                        return false;
                    }
                    break;
                default:
                    return false;
            }
        }
        return z == 2;
    }

    private void insertCharacter(char c) {
        kellah.push(c);
    }

    private Character readTopLetter() {
        char l = kellah.top();
        kellah.pop();
        return l;
    }
}

Nicht-deterministische Kellerautomaten

Bisher haben wir uns nur mit Kellerautomaten beschäftigt, deren Übergänge deterministisch sind. Genauso wie bei den bisher bekannten endlichen Automaten, kann man auch bei Kellerautomaten zwischen deterministisch und nicht-deterministisch unterscheiden.

Es gelten dabei die gleichen Regeln, wie bei anderen endlichen Automaten.

Im folgenden ist ein Nicht-deterministischer Kellerautomate (nPDA), welcher Palindrome erkennen kann, abgebildet.