Ein Deterministischer Endlicher Automat (DEA) überprüft eine Eingabemenge auf ihre Gültigkeit. Jeder DEA hat ein Eingabealphabet . Dieses gibt alle Zeichen an, die ein Automat akzeptieren kann. Das Eingabealphabet könnte beispielsweise folgendermaßen aussehen: .
Abhängig von der Eingabemenge wechselt ein Automat von einem Zustand in einen anderen.
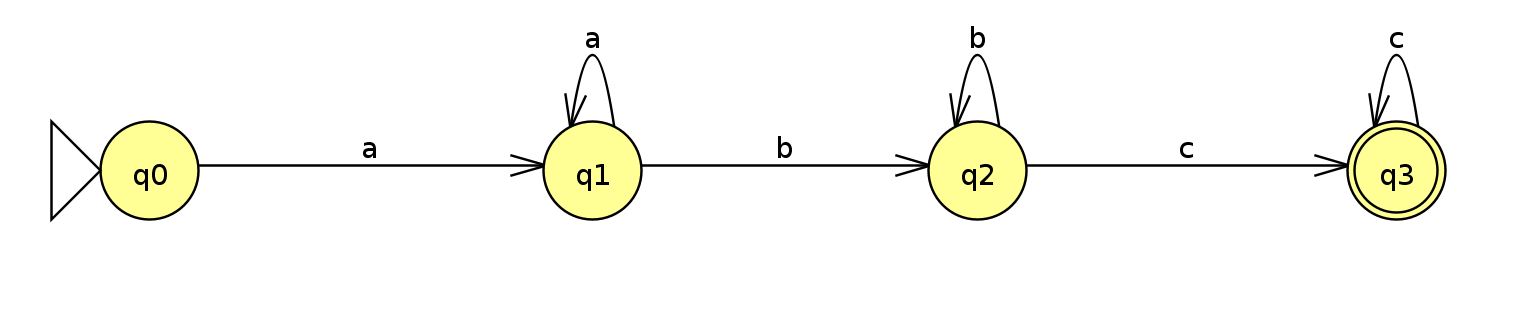
Das obige Bild zeigt einen Übergangsgraphen für einen DEA. Er besitzt als Eingabealphabet und überprüft, ob in der Eingabemenge alphabetisch sortiert ist und alle Buchstaben von a bis c enthält.
Eine gültige Eingabemenge wäre aabcc
Eine ungültige Eingabemenge wäre acb
Der Automat wird folgendermaßen beschrieben:
Die endliche Zustandsmenge:
Das Eingabealphabet:
Die Übergangsfunktion: = {
| a | b | c | |
|---|---|---|---|
| $$q_0$$ | $$q_1$$ | Senke | Senke |
| $$q_1$$ | $$q_1$$ | $$q_2$$ | Senke |
| $$q_2$$ | Senke | $$q_2$$ | Senke |
| $$q_3$$ | Senke | Senke | $$q_3$$ |
}
Der Startzustand:
endliche Menge an Endzuständen:
Um eine Eingabemenge nun mit dem Automaten zu validieren, wird über jedes Zeichen iteriert. Abhängig vom aktuellen Zustand, wird durch die Übergangsfunktion festgelegt, in welchen Zustand gewechselt werden muss.
Sollten noch nicht alle Zeichen im Automaten getestet worden sein, man aber schon am Endzustand angelangt sein, muss erst die gesamte Eingabemenge abgearbeitet werden. Wenn dann der aktuelle Zustand der Endzustand ist, kann die Eingabemenge als gültig betrachtet werden.
Das Beispiel geht außerdem davon aus, das alle nicht aufgeführten Übergänge in die Senke führen. Die Senke ist ein Fehlerzustand, der die Ungültigkeit einer Eingabemenge anzeigt.
Reguläre Ausdrücke
Reguläre Ausdrücke dienen dazu, die Sprache eines Automaten zu beschreiben. Mit der Sprache kann man alle Eingabemengen festlegen, die vom Automaten akzeptiert werden. Die Sprache für den oben dargestellten Automaten würde folgenderweise definiert werden.
steht in dieser Darstellung für einen valide Eingabemenge. Sie ist aus der Menge von zusammengesetzt. Also das Eingabealphabet in beliebiger Reihenfolge. Der zweite Teil der Definition sagt aus, dass eine valide Eingabe jedes Zeichen aus dem Eingabealphabet mindestens einmal enthalten muss.
Als regulärer Ausdruck wird nur der zweite Teil der Definition bezeichnet.
- : Menge aller Wörter, die man aus dem Alphabet bilden kann.
- : a kommt beliebig oft vor. a kann auch 0 mal vorkommen.
- : a kommt beliebig oft vor. a muss mindestens einmal vorkommen.
- : Es kommt a oder b vor.
Implementierung
Automaten können auch implementiert werden. Dabei wird der aktuelle Zustand als Integer gespeichert. Abhängig vom aktuellen Zustand und vom aktuellen Zeichen wird dann der Zustand gewechselt.
public static boolean parse(String text) {
int zustand = 0;
for (int i = 0; i < text.length(); i++) {
char zeichen = text.charAt(i);
switch (zustand) {
case 0:
if (zeichen == 'a') zustand = 1;
else return false;
break;
case 1:
if (zeichen == 'b') zustand = 2;
else if (zeichen == 'a') zustand = 1;
else return false;
break;
case 2:
if (zeichen == 'c') zustand = 3;
else if (zeichen == 'b') zustand = 2;
else return false;
break;
case 3:
if (zeichen == 'c') zustand = 3;
else return false;
break;
default:
return false;
break;
}
}
return zustand == 3;
}