Für jeden Automaten exisitert eine Sprache. Man kann diese durch durch einen regulären Ausdruck beschreiben. Eine weitere Möglichkeit eine Sprache eines Automaten zu beschreiben, stellt die Grammatik dar.

Als Beispiel für eine Grammatik lässt sich die deutsche Sprache nennen. Für sie gelten bestimmte Regeln:

<Satz>      ::= <Subjekt><Prädikat><Objekt>
<Subjekt>   ::= <Artikel><Substantiv>
<Objekt>    ::= <Artikel><Substantiv>

Man spricht hier von einer korrekten Syntax, die die Reihenfolge der sogenannten Nicht-Terminalsymbole beschreibt. Eine Grammatik beschreibt - nicht nur in dem Beispiel der deutschen Sprache - die korrekte Anwandung von Syntax und Semantik einer Sprache.

Allerdings lässt sich aus den obigen Regeln noch kein Satz bilden. Dafür werden sogenannte Terminalsymbole festgelegt. Sie “definieren” die Nicht-Terminalsymbole.

<Artikel>   ::= der | die | das
<Prädikat>  ::= spielen | essen | trinken
<Substantiv>::= Computer | Haus | Schule

Nicht-Terminalsymbole haben als Erkennungsmerkmal spitze Klammern.

Das Erstellen eines Satzes kann dann mit den Ableitungsregeln definiert werden.

<Satz> -> <Subjekt><Prädikat><Objekt>
       -> <Artikel><Substantiv><Prädikat><Artikel><Substantiv>
       -> Der <Substantiv><Prädikat><Artikel><Substantiv>
       -> Der Computer<Prädikat><Artikel><Substantiv>
...

Man erkennt, dass eine Verschachtelung der verschiedenen Nicht-Terminalsymbole entsteht, die bis hin zu den Terminalsymbolen geht. Man kann die Ableitungsregeln daher auch in einem Ableitungsbaum darstellen, bei dem die Blätter die Terminalsymbole sind.

Formale Definition einer Grammatik

Die Grammatik G setzt sich aus dem vier-Tupel $G=(N,T,R,S)$ zusammen.

$N$ ist die Menge an Nicht-Terminalsymbolen.
$T$ ist die Menge an Terminalsymbolen.
$R$ stellt die Ableitungsregeln dar.
$S$ ist das anfänliche Nicht-Terminalsymbol.

Beispiel

Es sei folgender Automat gegeben:

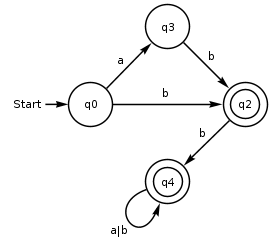
Ersetzt man die Zustände mit Nichtterminalsymbolen, kann man eine Grammatik $G$ erstellen, die eine valide Eingabe für den Automaten erzeugt.

N={S,A,B,C}

T={a,b}

R={
    S -> aB | bA
    A -> bC |b
    B -> bA
    C -> aC | bC | a | b
}
S=S

Da C den Zustand q4 beschreibt, müssen alle Übergänge, die zu diesem Zustand führen in der Grammatik durch ein Terminalsymbol dargestellt werden.

Eine Ableitung eines Wortes könnte folgendermaßen aussehen:

S -> aB -> abA -> abbC -> abbaC -> abbaa

Auch für Grammatiken kann eine formale Definition der Sprache vorgenommen werden:

Die obige Grammatik ist dabei links-linear. Das Wort wächst also immer von links nach rechts. Eine Grammatik, bei der das Wort von rechts nach links wächst wird dann rechts-linear genannt. Weiterhin handelt es sich um eine reguläre Grammatik, da alle Ableitungen ein Terminalsymbol enthalten.

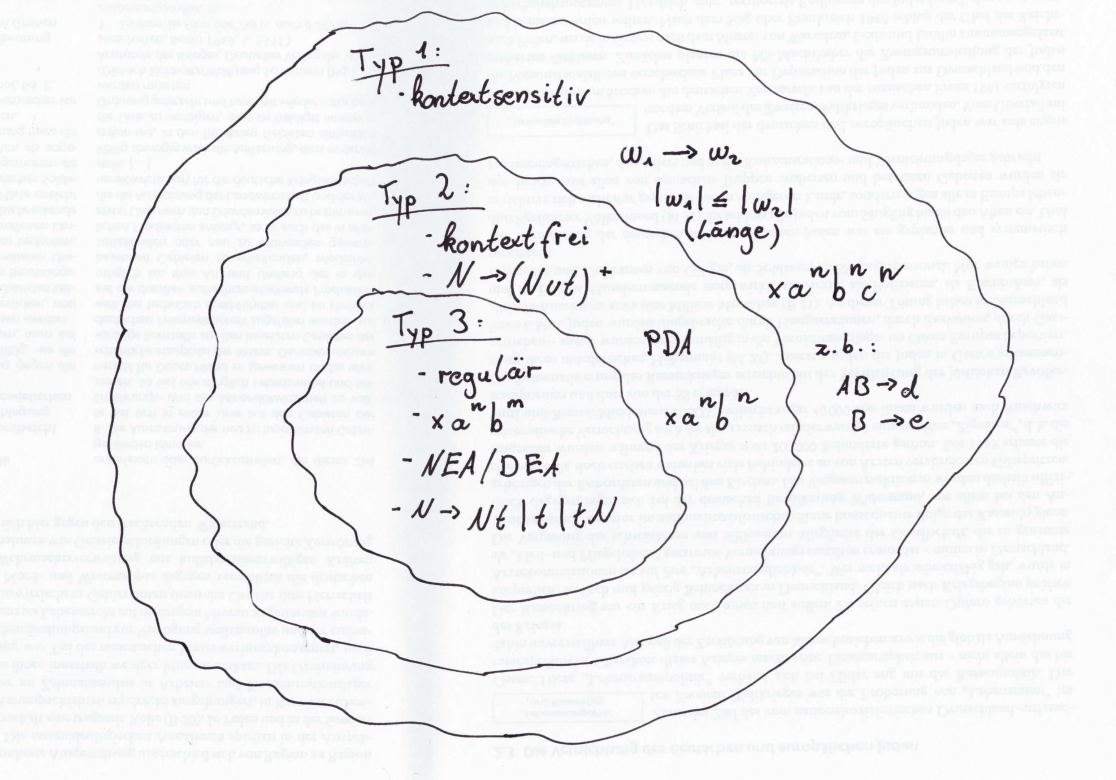
Grammatik-Typen

Grammatik lassen sich grundlegend in 3 Typen einteilen. Die folgende Grafik veranschaulicht die unterschiedlichen Definitionen der Typen.