Der Binäre Baum ist ein Beispiel für eine nichtliniare Datenstruktur.

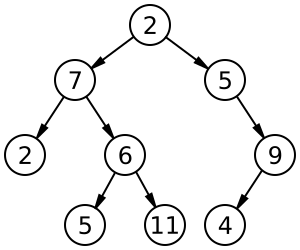By Derrick Coetzee (Own work), via Wikimedia Commons

Begriffe

Im folgenden werden die verschiedenen Begriffe eines Binärbaumes anhand des obigen Beispieles erklärt.

Knoten

Im obigen Bild sind die Kreise mit den Zahlen jeweils ein Knoten. Dieser Knoten sollte immer ein Inhaltsobjekt enthalten.

Wurzel

Der erste Knoten in einem Baum wird Wurzel genannt.

Kanten

Kanten sind die Verbindungslinien zwischen Knoten.

Blätter

Knoten, an denen kein weiterer Knoten hängt werden als Blätter bezeichnet.

Grad

Der Grad gibt die Anzahl der Nachfolger eines Knoten an. In einem Binären Baum darf jeder Knoten maximal einen Grad von 2 haben!

Pfad

Der Weg, den man von einem Knoten zu einem anderen Knoten gehen muss. In einem Binären Baum darf dieser nur von oben nach unten gehen.

Tiefe

Zählt man auf einem Pfad die Anzahl der Kanten, so ergibt sich daraus die Tiefe. Die Tiefe des längsten Pfades ist gleichzeitig auch die Tiefe des Baumes.

Ebene

Alle Knoten, die den gleichen Abstand zur Wurzel haben sind auf einer Ebene zu finden.

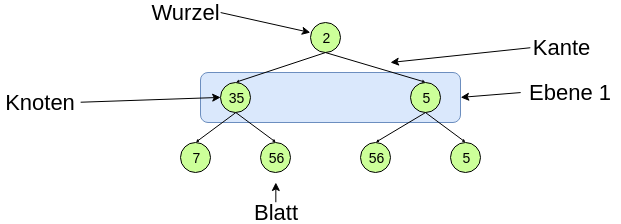
Beim Benutzen des binären Baumes muss darauf geachtet werden, dass man innerhalb des Baumes nicht wieder zurückgeht oder auf einer Ebene zwei Knoten auf einem Pfad anspricht. Der Baum ist also azyklisch. Die Knoten sind also nicht innerhalb einer Ebene miteinander verbunden.

Implementierung

Für eine einfachere Implementierung muss beachtet werden, dass die Teilbäume jeweils auch binäre Bäume sind. Folgendes Bild verdeutlicht diesen Ansatz:

Quelle: https://www.sqa.org.uk/e-learning/LinkedDS04CD/page_30.htm

Attribute

Aus diesem Grund sind in dem Objekt BinaryTree folgende Attribut zu finden.

private CT content;
private BinaryTree<CT> leftTree;
private BinaryTree<CT> rightTree;

Auch bei dieser Datenstruktur wird wieder ein generischer Datentyp verwendet. Ihn kann man mit CT ansprechen.

Konstruktoren

Das Objekt kann mit drei unterschiedlichen Konstruktoren erzeugt werden. Es ist dabei zu beachten, dass ein leerer Baum dennoch als Objekt existiert. Lediglich seine Attribute sind null.

1.leeren Baum erzeugen.

public BinaryTree() {
    content = null;
    leftTree = null;
    rightTree = null;
}

2.Baum nur mit einem Inhaltsobjekt erzeugen. Sollte dabei der übergebene Inhalt null sein, so wird ein leerer Baum erzeugt.

public BinaryTree(CT pContent) {
    if (pContent != null) {
        content = pContent;
        leftTree = new BinaryTree<CT>();
        rightTree = new BinaryTree<CT>();
    } else {
        content = null;
        leftTree = null;
        rightTree = null;
    }
}

3.Es wird ein Baum erzeugt, der sowohl ein Inhaltsobjekt, als auch zwei Teilbäume besitzt.

public BinaryTree(
            CT pContent, 
            BinaryTree<CT> pLeftTree, 
            BinaryTree<CT> pRightTree
                ) {
    if (pContent != null) {
        content = pContent;

        if (pLeftTree == null) leftTree = new BinaryTree<CT>();
        else leftTree = pLeftTree;

        if (pRightTree == null) rightTree = new BinaryTree<CT>();
        else rightTree = pRightTree;
    } else {
        content = null;
        leftTree = null;
        rightTree = null;
    }
}

Methoden

Alle weitere Methoden sind unten dargestellt.

public boolean isEmpty() {
    return content == null;
}

public void setContent(CT pContent) {
    if (pContent != null) {
        if (isEmpty()) {
            leftTree = new BinaryTree<CT>();
            rightTree = new BinaryTree<CT>();
        }
        content = pContent;
    }
}

public CT getContent() {
    return content;
}

public void setLeftTree(BinaryTree<CT> pLeftTree) {
    if (!isEmpty() && pLeftTree != null) {
        leftTree = pLeftTree;
    }
}

public void setRightTree(BinaryTree<CT> pRightTree) {
    if (!isEmpty() && pRightTree != null) {
        leftTree = pRightTree;
    }
}

public BinaryTree<CT> getLeftTree() {
    if (isEmpty()) return null;
    return leftTree;
}

public BinaryTree<CT> getRightTree() {
    if (isEmpty()) return null;
    return rightTree;
}

Traversierung

Traversierung ist in der Graphentheorie der Name für Verfahren, die eine Route bestimmen, bei der jeder Knoten und jede Kante eines baumförmigen Graphen genau einmal besucht wird.

via Wikipedia

Eine Traversierung ist beispielsweise dann nötig, wenn ich den Baum nach einen speziellen Wert durchsuchen muss. Dabei stoßen wir aber auf ein Problem: Wir wissen zwar immer den Nachfolger eines Knotens, aber nicht den Vorgänger. Für uns bedeutet das, dass wir aus einem Teilbaum nich in den anderen Teilbaum kommen, nachdem wir einen Teilbaum durchsucht haben.

Die Lösung für das Problem liegt in der Rekursion. Durch sie können wir für jede Rekursionstiefe eine Ebene eines Teilbaumes durchsuchen.

Bei der Traversierung unterscheidet man zwischen drei unterschiedlichen Verfahren:

Preorder-Traversierung

Eine Preorder-Traversierung zeichnet sich dadurch aus, dass man sich immer zuerst die Wurzel und dann den linken- und anschließend den rechten Teilbaum anschaut.

besuche (baum b):
    SPEICHERE Inhalt
    FALLS linker Teilbaum von b existiert:
        besuche(linker Teilbaum von b)
    FALLS rechter Teilbaum von b existiert:
        besuche(rechten Teilbaum von b)

Inorder-Traversierung

Bei der Inorder-Traversierung wird zuerst der linke Teilbaum, dann die Wurzel und dann der rechte Teilbaum betrachtet.

besuche (baum b):
    FALLS linker Teilbaum von b existiert:
        besuche(linker Teilbaum von b)
    SPEICHERE Inhalt
    FALLS rechter Teilbaum von b existiert:
        besuche(rechten Teilbaum von b)

Postorder-Traversierung

Bei der Postorder-Traversierung wird die Wurzel als letztes betrachtet.

besuche (baum b):
    FALLS linker Teilbaum von b existiert:
        besuche(linker Teilbaum von b)
    FALLS rechter Teilbaum von b existiert:
        besuche(rechten Teilbaum von b)
    SPEICHERE Inhalt

Beispiel für eine Traversierung

Ein Beispiel, einer Traversierung eines Baumes sähe folgendermaßen aus.

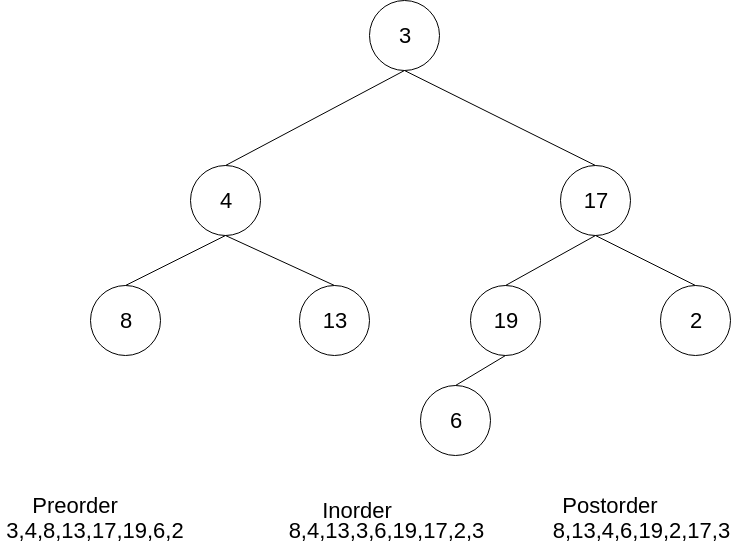
Erweiterung der Möglichkeiten…

Da die Abiturklasse des BinaryTree keine Möglichkeiten zur Traversieung hat, haben wir unsere eigene Klasse geschrieben um die Traversierung mehrmals benutzen zu können. In dieser sind nicht nur die Methoden zum Traversieren, sondern auch Methoden um die Tiefe und Größe eines Baumes zu bestimmen.

Weiterhin ist auch die Möglichkeit vorhanden, dass aus einer gegebenen Preorder und Inorder Traversierung ein Baum erzeugt wird gegeben. Die Inorder und Preorder Traversierung werden dabei als Listen angegeben. Diese haben dabei insbesondere durch die einfache Möglichkeit zum Iterieren einen Großen Vorteil bei dieser speziellen Anwendung.

Aus Inorder und Preorder Reihe Baum erzeugen

Im Folgenden wird der Pseudocode dargestellt, um einen neuen Baum aus einer Preorder und Inorder Traversierung zu erzeugen.

Speichere Inorder und Preorder in Listen

func inPre(preorder, inorder)

    WENN preorderListe oder inorderListe leer ist
        GIB leeren Baum zurück

    NEHME erstes Element aus Preorder und nenne es content
    LÖSCHE content aus Preorder

    SUCHE content in InorderListe

    Alle Elemente in InorderListe links von content gehöhren dem linken Teilbaum an.
    Alle Elemente in InorderListe rechts von content gehören dem rechten Teilbaum an.
    
    LÖSCHE content aus PreorderListe

    TEILE preorderd in linken und rechten Teil ein.

    linkerTeil = inPre(preorderlinks, links)
    rechterTeil = inPre(preorderrechts, rechts)

    GIB neuen Baum mit content als Content und linkerTeil als linker Teilbaum und rechterTeil als rechterTeilbaum zurück

Quelle: http://knowyourmeme.com/photos/1272773-if-a-dog-wore-pants