Bislang war der Datenverkehr, der über unsere Server Anwendungen lief, nicht verschlüsselt. Grundsätzlich war dies kein Problem, da kein sensibler Inhalt über das Netzwerk übertragen wurde. Sollte jetzt aber beispielsweise ein Anmeldefeature bei einer Anwendung benötigt werden, so sollte wenigstens das Passwort des Clients verschlüsselt werden, da sonst unbekannte Dritte einfach den Netzwerkverkehr überwachen müssten, um dabei zufällig auf das Passwort zu stoßen.
Kryptologie ist in der heutigen Zeit nich mehr wegzudenken. In einem früheren Beitrag bin ich schon auf zwei Verschlüsselungsverfahren eingegangen. Der Beitrag kann hier gelesen werden.
Aufbau der Kommunikation
Unsere Kommunikation lässt sich folgendermaßen darstellen:
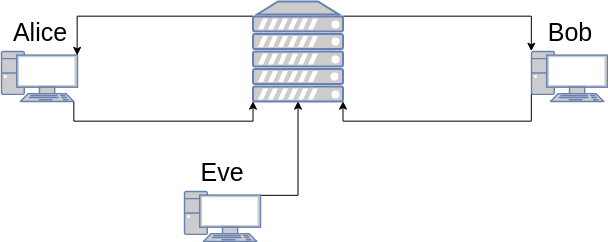
Dabei haben wir drei Akteure: Alice und Bob sind die beiden Clients, die miteinander kommunizieren wollen. Da ihre Unterhaltung sensible Daten beinhaltet, wollen sie ihren Datenverkehr verschlüsseln. Eve stellt dabei den Beobachter dar, der alle Daten die über das Netzwerk gesendet werden, lesen kann.
Der Austausch des Schlüssels
Verschlüsselungsverfahren erfordern in den meisten Fällen einen Schlüssel. Doch wie können sich zwei Clients (in unserem Fall Alice und Bob) auf einen Schlüssel einigen, ohne dass Eve diesen Schlüssel mitlesen kann? Sobald ein Angreifer den Schlüssel zu einer kodierten Nachricht kennt, sind gesendete Nachrichten nicht mehr sicher. Logischerweise sollte daher ein sicheres Schlüsselaustauschverfahren verwendet werden.
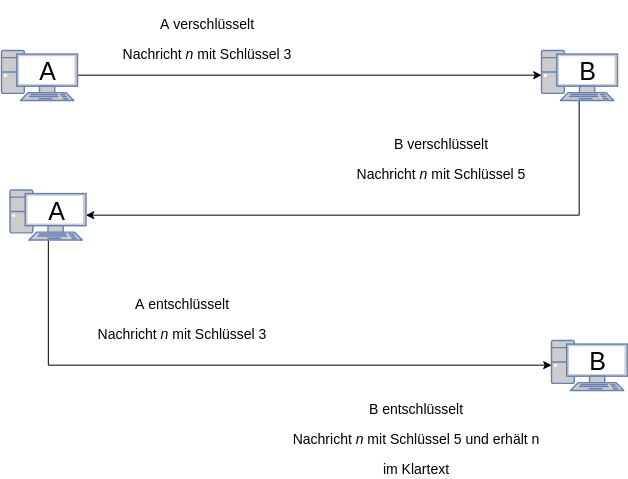
Wie das obige Bild zeigt, sind mehrere Ver- und Entschlüsselungen der Nachricht nötig, bis beide Seiten die gleiche Nachricht in Form das Schlüssels bekommen haben.
Die Verschlüsselungsverfahren, die zum verschlüsseln der Nachricht n benutzt werden, können jedoch nicht frei gewählt werden. So ist beispielsweise die Caeser Verschlüssung bei dem Schlüsselaustausch möglich, ein Angreifer kann jedoch sehr einfach die Schlüssel rausfinden, die die beiden Anwender jeweils benutzt haben. Daher bietet sich dieses Verfahren nicht an. Im Gegensatz ist das Verfahren der Substitution nicht möglich, da beide Anwender völlig unterschiedlich und willkürlich verschlüsseln.
Schlüsselaustausch nach Diffie und Hellman
Auch die beiden Kryptologen Whitfield Diffie und Martin Hellman veröffentlichten 1976 ein Verfahren, dass auf dem oben beschriebenen Schlüsseltausch basiert.
Das obige Bild zeigt das Schlüsselaustauschverfahren nach Diffie und Hellman anhand von Farbeimern. Dabei wird ein Schlüssel in Form der Farbe Grün generiert, der für beide Beiteiligten gleich ist, ohne dass ein Außenstehender diesen Schlüssel ebenfalls erstellen kann.
Um dieses Verfahren in der Praxis umzusetzen, wird folgendes Protokoll befolgt:
- Alice und Bob einigen sich öffentlich auf eine Primzahl und eine natürliche Zahl .
- Nun wählen Alice und Bob je eine weitere Zahl , die sie jeweils geheim halten. Eve kennt nun die Zahlen und .
- Anschließend berechnet Alice und Bob
- Alice und Bob tauschen die Zahlen A und B aus. Eve kennt die Zahlen A und B.
- Dannach berechnet Alice den Schlüssel und Bob den Schlüssel
Es sollte nun gelten:
Als Beweis, dass beide Seiten den selben Schlüssel errechnen gilt:
Implementierung
Für die Anwendung des oben beschriebenen Verfahrens, wird dieses in Java umgesetzt.
public DiffieHellman(int pBitLength) {
this.bitLength = pBitLength;
}
public BigInteger createProbablePrime() {
SecureRandom rnd = new SecureRandom();
return BigInteger.probablePrime(bitLength, rnd);
}
public String generateP(String txtP) {
if (txtP.isEmpty()) {
this.p = this.createProbablePrime();
} else {
this.p = new BigInteger(txtP);
}
return this.getP().toString();
}
public String generateG(String txtG) {
if (txtG.isEmpty()) {
Random rand = new Random();
this.g = BigInteger.valueOf(rand.nextInt(this.getP().intValue()) + 1);
} else {
this.g = new BigInteger(txtG);
}
return this.getG().toString();
}
Nachdem ein DieffieHellman-Objekt erzeugt wurde, sollten die Methoden generateP() und generateG() aufgerufen werden. Sie erzugen die Zahlen und . Zum Erzeugen einer Primzahl kann die Methode probablePrime() der Klasse BigInteger verwendet werden. Alle erzeugten Werte werden dabei als BigInteger gespeichert, da dieser Datentyp längere Integers ermöglicht, und damit eine bessere Sicherheit.
Einige Methoden bekommen einen String übergeben. Sollte dieser leer sein, wird von der Methode der jeweilige Wert generiert. Andernfalls wird der Wert übernommen.
public String generatePrivateA() {
if (this.getP().toString().isEmpty()) return "";
Random rand = new Random();
this.privateA = BigInteger.valueOf(rand.nextInt(this.getP().intValue()) + 1);
return this.getPrivateA().toString();
}
public String generatePublicA() {
if (
this.getG().toString().isEmpty() ||
this.getP().toString().isEmpty() ||
this.getPrivateA().toString().isEmpty()
)
return "";
this.publicA = getG().pow(this.getPrivateA().intValue()).mod(this.getP());
return this.getPublicA().toString();
}
public String generateKey(String txtB) {
if (txtB.isEmpty()) return "";
BigInteger b = new BigInteger(txtB);
this.key = b.pow(this.getPrivateA().intValue()).mod(this.getP());
return this.key.toString();
}
Auch alle weiteren Methoden funktionieren nach dem selben Prinzip und sind deshalb manuell aufzurufen.
Sicherheitsrisiken
Natürlich ist das Verfahren nicht gänzlich gegen Angriffen gesichert. Eine mögliche Sicherheitslücke entsteht, wenn die unbekannte dritte Person Eve und kennen sollte. In diesem Fall kann Eve einfach den Schlüssel ausrechnen. Zusätzlich kommt hinzu, dass alle Zahlen, die man wählt (insbesondere und , sowie die Primzahl ) Zahlen mit hohen Dezimalstellen sein sollten. Ansonsten kann ein Computer die Zahlen durch Bruteforce sehr leicht rausfinden.
Man-in-the-middle Angriff
Der Man-in-the-middle (MitM) Angriff ist insbesondere bei dem Diffie-Hellman Verfahren gefährlich und kann dazu führen, dass ein Angreifer angeblich verschlüsselte Kommunikation zwischen zwei Personen mitlesen kann, ohne dass diese Personen von dem Angriff wissen.
Bei dem Angriff glauben die Personen Alice und Bob, dass sie miteinander einen Schlüsselaustausch nach Diffie-Hellman vornehmen. Dabei haben sie jedoch jeweils einen Schlüsselaustausch mit dem Angreifer gemacht. Dieser kann nun eine von Alice gesendete Nachricht entschlüsseln, sowie lesen und verändern und dann mit dem Schlüssel, der mit Bob ausgetauscht wurde, die Nachricht an Bob weitersenden.
Die folgende Grafik veranschaulicht das Prinzip einer MitM-Attacke. Dabei ist eine Zahl, bei der gilt: . Sie ist damit vergleichbar mit den Zahlen und .

Damit sich Alice und Bob gegen eine solche Attacke schützen können, ist die beste Möglichkeit, sich gegenseitig zu verifizieren. Dabei kann Bob beispielsweise sicher sagen, dass die Nachricht von Alice auch wirklich von ihr kommt, und nicht von einer unbekannten dritten Person.