Um die Rekursion zu verstehen muss man die Rekursion verstehen…
In den letzten Unterrichtsstunden haben wir uns anhand der Türme von Hanoi mit der Rekursion beschäftigt:
Türme von Hanoi
Wir wollen aber mal ganz von vorne anfangen und die Regeln sowie das Spiel an sich verstehen, bevor wir uns mit der Rekursion beschäftigen.
 Quelle: https://de.wikipedia.org/wiki/Datei:Tower_of_Hanoi.jpeg
Quelle: https://de.wikipedia.org/wiki/Datei:Tower_of_Hanoi.jpeg
Wie in der obigen Abbildung zu erkennen, gibt es drei Stäbe. Im Ausgangszustand sind auf einem der drei Stäbe unterschiedlich große Scheiben, von groß nach klein, aufgesteckt. Ziel des Spieles ist es, dass alle Scheiben in der selben Form auf einem der beiden anderen Stäbe stecken. Dabei ist jedoch zu beachten, dass beim Umschichten der einzelnen Scheiben keine größere Scheibe auf einer kleineren Scheibe liegen darf. Folgende Animation verdeutlicht das Prinzip mit vier Scheiben.
 Quelle: https://de.wikipedia.org/wiki/Datei:Tower_of_Hanoi.gif
Quelle: https://de.wikipedia.org/wiki/Datei:Tower_of_Hanoi.gif
Züge:
Im Unterricht ging es nun darum die Anzahl der Züge zu berechnen, die man für jede Scheibe braucht. Dafür hat man dann erst die Anzahl der Züge für verschiedene Scheiben in eine Tabelle eingetragen, aus diesen Werten konnte man dann zwei Formeln finden.
| Scheiben $$ n $$ | Schritte $$ Z(n) $$ |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 3 |
| 4 | 15 |
| 5 | 31 |
| 6 | 63 |
| 7 | 127 |
| $$ n $$ | $$ Z(n) = 2^n-1 $$ |
| $$ Z(n) = 2 * Z(n-1) + 1 $$ |
Die erste der beiden Formeln sollte soweit logisch sein, genauso wie der Weg sie zu implementieren:
static int HanoiImplizit(int n){ //Implizite Methode zum direkten Berechnen
double cache = Math.pow(2,n)-1 ;
return (int) cache;
}Die Methode bekommt als Parameter die Anzahl der Scheiben übergeben, aus denen sie dann die Anzahl der Schritte berechnet. Math.pow() ist dabei eine von Java mitgelieferte Methode, die eine Basis und einen Exponenten (in der genannten Reihenfolge) übergeben bekommt, und diesen dann als double Datentyp zurückgeht. Dabei ergibt sich auch schon das Problem, dass wir eigentlich als Rückgabewert einen Integer haben wollen, weshalb wir den Wert der Math.pow() Methode auch in eben diesen umwandeln.
Für die zweite und auch die deutlich interessantere Formel muss man sich folgendes überlegen: Ich habe beim Umschichten immer das selbe Prinzip, bei dem ich versuche die unterste Scheibe auf einen anderen Stab zu bekommen. Habe ich das geschafft, so versuche ich aus den verbleibenden Scheiben die Unterste auf die eben aussortierte Scheibe zu bekommen(siehe Animation). Wir erkennen also einen wiederkehrenden Vorgang. Selbiges kann man auch in der zweiten Formel erkennen. Einen solchen Ablauf nennt man Rekursion, der ein sich selbst wiederholender ist.
Soll nun eine solche Rekursive Methode implementiert werden, so muss man sich über den Ablauf im klaren werden.
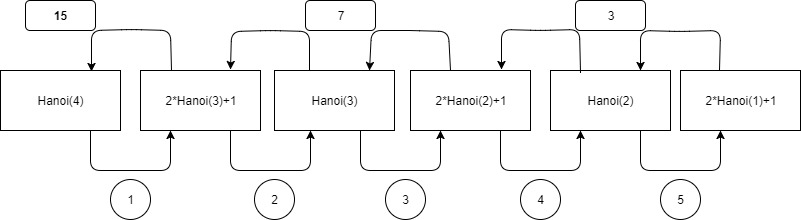
In dem obigen Schaubild (Aufrufprotokoll) ist zu erkennen, dass die Methode Hanoi bis zu dem Punkt (der Rekursionstiefe) aufgerufen wird, bis n 1 beträgt. Das liegt daran, dass das Programm weiß, dass bei einer Scheibe auch nur ein Zug gebraucht wird.
if(n == 1) {
return 1;
}Sollte also das Programm bei n = 1 angekommen sein, so können die einzelnen aufgerufenen Methoden( hier in den mittleren Kästen) ihre Anzahl der Züge zurückgeben (die oberen Pfeile in dem Aufrufprotokoll). Dies geschieht bis man wieder zurück bei Hanoi(4) ist. Diese Methode gibt dann 15 als Anzahl der Züge zurück. Aus der Sicht des Quelltextes bedeutet das, sollte n größer als 1 sein, die Methode sich selbst noch einmal aufrufen muss. Dann aber mit einer Scheibe weniger, damit wir bis zu n=1 kommen und dann die Methoden ihr Ergebnis an die über ihr stehende Methode zurückgeben kann. Das ganze sieht im Code dann folgendermaßen aus:
static int Hanoi(int n){ //Rekursive Methode
if(n == 1) {
return 1;
}else {
return 2*Hanoi(n-1) +1;
}
}Hiermit haben wir nun die ersten rekursiven Schritte gemacht.