Fibonacci:

Fibonacci war einer der wichtigsten Mathematiker des Mittelalters, der unter anderem die Fibonacci Abfolge entwickelt hat. Diese ist eine theoretisch unnendlich weitergehende Zahlenfolge, die in unserem Fall Rekursiv erstellt wird.

Prinzip:

$$ 1,1,2,3,5,8…$$

Die obige Zahlenreihe stellt den Anfang der Abfolge dar: Um immer zur nächsten Zahl zu kommen addiere ich die beiden vorherigen Zahlen. Das heißt dann, dass ich, um auf 2 zu kommen, 1 und 1 addieren muss. Und für 3 dann 1 und 2.

Die Formel beschreibt genau diesen Rekursiven Ansatz. Dabei muss man in Fällen lesen: Entweder n ist größer 1 (oben), oder kleiner/gleich (unten). Sollte der erste Fall eintreten, so muss man die rekursive Methode anwenden. Tritt der zweite Fall ein, so ist Z(n) = 1. Das gleiche kann man auch an der oben abgebildeten Reihe erkennen: An der nullten und ersten Stellen ist das Ergebnis eins, wohingegen sich das Ergebnis nach den ersten beiden Stellen ändert.

Um das ganze nun zu implementieren ist das System ähnlich zu den Türmen von Hanoi. Ich überlege mir erst die Basis:

Sollt n (die Anzahl der Züge) gleich 0 oder 1 sein, so weiß ich, dass Z(0) und auch Z(1) als Ergebnis 1beziehungsweise n haben.

if(n < 2){      
    return n;
}

Um nun den Rekursionsschritt, also den obigen Teil der Formel, zu implementieren, ruft man einfach nochmal die Methode mit der oben gegebenen Formel auf und gibt ihr Ergebnis zurück.

else{
    return fibonacci(n-1) + fibonacci(n-2);
}

Schon haben wir unsere Rekursive Methode implementiert. Wir können nun aus einer Formel direkt die Implementierung erkennen, da wir in der Formel Basis und Schritt gegeben haben.

Aufrufprotokoll

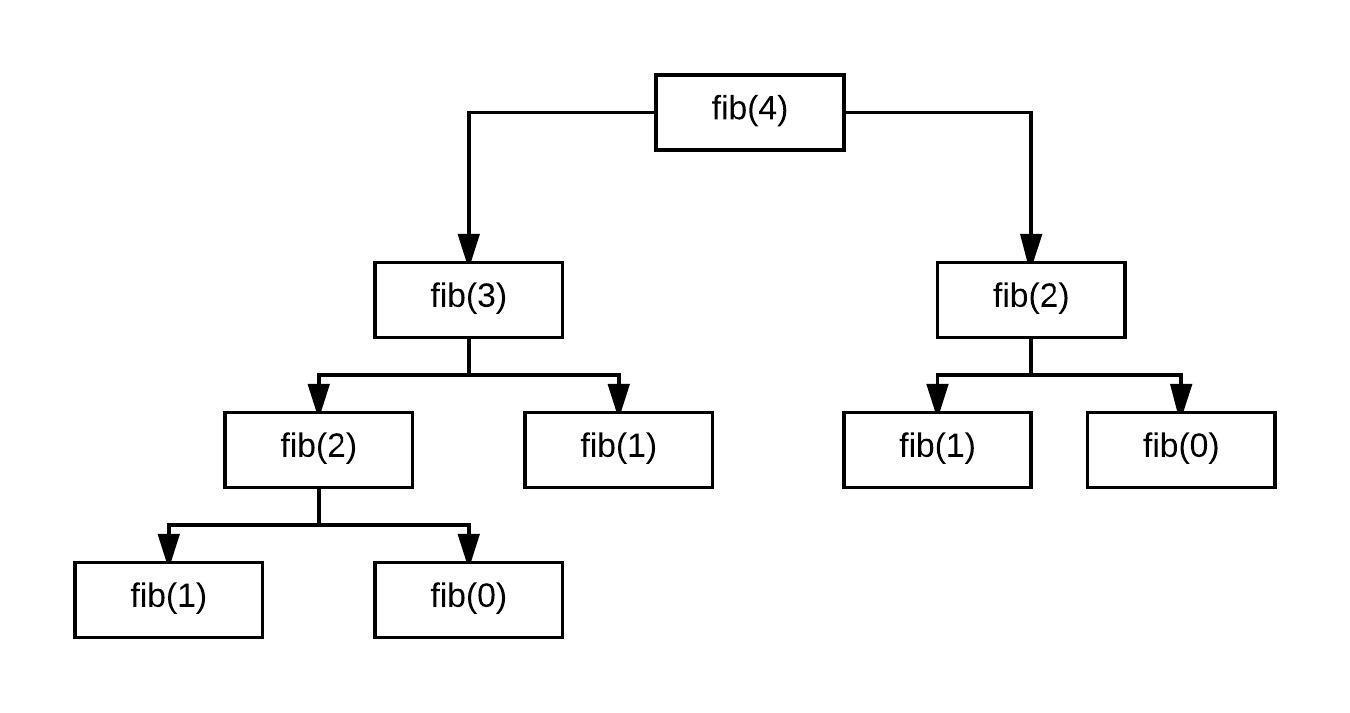
Einen rekursiven Vorgang wie zum Beispiel die Fibonacci-Folge kann man auch in einem sogenannten Aufrufprotokoll darstellen, in dem die rekursiv aufgerufenen Methoden jeweils in eine neue Ebene kommen, und dann mit Pfeilen mit der vorhergehenden Methode verbundenen werden. Dieses Aufrufprotokoll gibt dann zum Beispiel Aufschluss drüber, wie tief die Rekursion geht. Aber in diesem Fall kann man auch erkennen, dass die Methoden  mehrmals aufgerufen werden. Deshalb bietet es sich an, dass man versucht, die Ergebnisse der schon einmal aufgerufenen Methoden beispielsweise in einem Array oder ähnlichen zwischenzuspeichern. Dafür habe ich eine ArrayList in der Klasse initialisiert. Diese hat den Vorteil, dass man in ihr unendlich viele Werte speichern kann.

public static List<Integer> gebraucht= new ArrayList<>(Arrays.asList(0,1));

Dabei speichere ich mit Arrays.asList(0,1) schon für den Index null und eins, die Ergebnisse eins. Deshalb fängt auch diese Method bei eins an zu zählen und nicht bei null.

static int fibonacciListe(int n){
    if(gebraucht.size() <= n ){
        gebraucht.add(n,fibonacciListe(n-1) + fibonacciListe(n-2));
        return gebraucht.get(n);
    } else{
        return (gebraucht.get(n));
    }

}

Die Methode fibonacciListe bekommt wie schon auch bei der letzten Methode die Anzahl  der Schritte übergeben, die sie berechnen soll. Wir sortieren nun unsere Methode ohne Zwischenspeicher ein wenig um, sodass zuerst mit gebraucht.size() <= nüberprüft wird, ob der gesuchte Wert zu n schon in dem Array enthalten ist. Sollte die Liste nicht so lang wie n sein und somit den Wert zu n nicht enthalten, so muss man an der Stelle von n der Wert mit gebraucht.add einfügen. Dafür gibt man als Index n und als Wert den rekursiven Methodenaufruf, den man schon von der obigen einfachen Methode kennt, an. Danach kann der Wert mit gebraucht.get(n) von nzurückgeben werde. Sollte jedoch der Wert schon in dem Array enthalten sein, so muss man ihn nur noch zurückgeben. Das ganz spart also viel Zeit und Rechenleistung, was einen tiefere Rekursion ermöglicht.

Hofstadter Funktion

Eine weitere rekursive Folge bildet die Hofstadter Q-Folge. Die von dem Informatiker Douglas R. Hofstadter (*1945) entwickelt wurde. Sie beschreibt eine weiterentwickelte Fibonacci Folge, die aber auf dem selben Prinzip beruht.

$$ 1,1,2,3,3,4…$$

Die obige Folge wird mit folgender Formel gebildet:

Die obige Formel beginnt eigentlich bei eins zu zählen, da wir aber auch beispielsweise in einem Array bei null anfangen zu zählen, habe ich auch die Formel auf diese Weise angepasst. Nun ist es einfacher auch die Implementierung zu gestalten, da man einfach das Prinzip anwenden muss, dass man schon bei der Fibonacci-Folge angewandt hat. So haben wir unten wieder die Basis stehen: Sollte die Anzahl der Schritte null oder eins betragen, ergibt die Formel 1. Ist dies nicht der Fall, wird die Formel, wie in dem obigen Teil rekursiv aufgerufen.

In der Implementierung sieht das dann folgendermaßen aus

private static int hofRek(int n){
    if(n > 2){
        return hofRek(n-hofRek(n-1)) + hofRek(n-hofRek(n-2));
    }else{
        return 1;
    }
}