Die Rekursion, die in dem letzten Artikeln eingeführt wurde, kann auch grafisch dargestellt werden. Als Beispiel dafür haben wir uns die Kochkurve angeschaut.
Die Kochkurven wurden von dem schwedischen Mathematiker Helge von Koch, der von 1870 - 1924 lebte entwickelt.
Die obige Kochkurve zeigt ein mögliches Beispiel, dass wir am Ende dieses Blogs auch erstellen können. Dazu müssen wir uns aber erst einmal mit dem Aufbau einer solchen Kurve beschäftigen, um sie dann später in den Quelltext zu implementieren.
Also was genau ist denn eine Kochkurve, und wie entscheide ich, wie viele ich jetzt aneinander setze? Diese Frage ist so nicht zu beantworten, da es nicht die eine Kochkurve bei unserem Beispiel gibt. Wir lösen dieses Problem, wer hätte es gedacht, Rekursiv. Nun haben wir aber nicht mehr irgendwelche Formeln, sondern sind im Bergriff grafisch zu zeichnen.
Prinzip Kochkurven:
Quelle: AB3 - Rekursive Kurven.docx (Unterricht)
Anstatt die Basis in einer Formel darzustellen, stellen wir sie grafisch dar. Wie haben also als Basis, auch Initiator genannt, einen geraden Strich. Im nächsten Teil wird jeder dieser Striche in drei Teile geteilt, und damit dann die Tiefe 1 erzeugt, die auch Generator genannt wird. Das malen einer Tiefe würde dann im Prozedere folgendermaßen aussehen.
Grundlaenge laenge
male gerade mit laenge/3
drehe 60 Grad nach links
male gerade mit laenge/3
drehe 120 Grad nach rechts
male gerade mit laenge/3
drehe 60 Grad nach links
male gerade mit laenge/3
Man hat nun aus dem Initiator die Tiefe 1 geschaffen. Um nun zur nächsten Tiefe zu kommen, muss man das obige Vorgehen auf jede einzelne Linie in der Tiefe 1 anwenden. Das ganze kann dann beliebig oft fortgeführt werden.
Die Rekursion ist dabei in jeder einzelnen Linie versteckt, die, wenn sie sich noch nicht in der Zieltiefe befindet die Methode malen noch einmal aufruft.
Dieses Prinzip kann man nun auf den Code anwenden:
public void zeichneKoch1(int t, double laenge) {
double a = laenge;
if (t == 0) {
turtle.forward(a);
} else {
zeichneKoch1(t - 1, a / 3);
turtle.left(60);
zeichneKoch1(t - 1, a / 3);
turtle.right(120);
zeichneKoch1(t - 1, a / 3);
turtle.left(60);
zeichneKoch1(t - 1, a / 3);
}
}Wir haben von Herrn Reichelt ein Raster bekommen, dass eine GUI beinhaltet. Um nun tatsächlich malen zu können, benutzen wir eine Bibliothek namens Turtle, die eine malende Schildkröte zu dem Programm hinzufügt.
Hierbei bekommt die Methode die Rekursionstiefe und die Länge als Parameter übergeben. Zuerst habe ich mich dann für das einfachere Verständnis dafür entschieden, dass ich meine Länge a nenne. Sollte die Rekursionstiefe t 0 betragen, so brauche ich nur meinen Initiator zeichnen. Sollte das nicht der Fall sein, so benutzt man den obigen Pseudocode rekursiv um die Tiefe 1 zu Zeichnen. Das geschieht so lange, bis t-1 = 0 beträgt.
Schneeflocke
Eine Weiterentwicklung der Kochkurve ist die Schneeflocke.
Offensichtlich ist beim genauen Hinschauen, dass wir hier auch wieder die Kochkurven drin versteckt haben. Deshalb können wir auch hierbei die zeichneKoch1()Methode anwenden, wobei wir uns ein Dreieck vorstellen müssen, wo an jeder Seite die zeichneKoch1() Methode durchgeführt wird.
public void schneeflocke(int t, double laenge) {
double a = laenge;
zeichneKoch1(t, a);
turtle.right(120);
zeichneKoch1(t, a);
turtle.right(120);
zeichneKoch1(t, a);
turtle.right(120);
}Drachenkurve
Die dann doch etwas andere Kurve, wenn man sie so nennen möchte, ist die Drachenkurve. Diese ist zwar auch Rekursiv aufgebaut, beruht aber auf einer anderen Methodik, als die beiden vorher genannten Kurven.
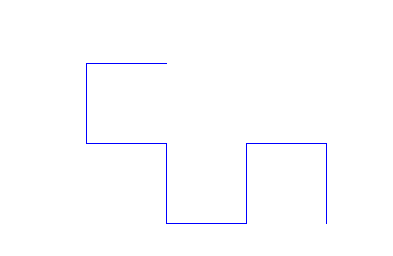
Um diese Art von Kurven zu verstehen, ist es von wichtig, sich den Initiator und den darauffolgenden Generator anzuschauen:
Initiator:
Der Initiator ist eine Einfache Linie, die von links nach rechts mit der angegebenen Länge gezeichnet wird.
Generator:
Der Generator (hier mit der Tiefe 1) wird so aufgebaut, dass wir zuerst den Initiator zeichnen, uns dann um 90° nach links drehen und dann wieder den Initiator zeichnen. Darin liegt auch die Rekursion: Wie zeichnen zuerst den einen Teil mit einer Rekursionstiefe von t-1 und drehen uns um 90° nach links und zeichnen nochmal mit der Rekursionstiefe t-1.
Drachenkurve Rekursionstiefe 2
Da wir uns aber mit diesem bisherigen Prinzip immer im Kreis bewegen, müssen wir noch ein Vorzeichen einführen. Das bedeutet dann, dass wir die eine Hälfte mit 90° zeichnen, die andere Hälfte aber mit -90°. Nimmt man die Rekursionstiefe 2, so wird dieses Problem deutlicher, da wir sonst ein Quadrat zeichnen würden, weil die unterste Linie in die entgegengesetzte Richtung zeigen würde.
public void zeichneDrachen(int t, double vz, double laenge) {
double a = laenge;
int alpha = 90;
if (t == 0) {
turtle.forward(laenge);
} else {
zeichneDrachen(t - 1, 1, a);
turtle.left(alpha * vz);
zeichneDrachen(t - 1, -1, a);
}
}Pythagoras Baum:
Der Pythagoras Baum ist ein weitere rekursive Zeichnung, die sich aus dem graphischen Beweis für den Satz des Pythagoras herleitet.
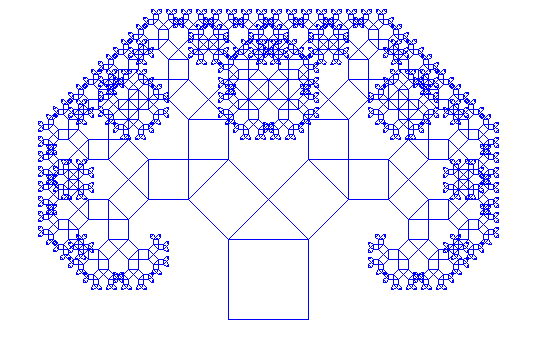Beispiel für einen Pythagoras Baum mit der Tiefe 10
Wie man oben schon in Ansätzen erkenne kann, haben wir Ein großes Quadrat mit der Länge laenge und zwei kleine Quadrate mit der Länge laenge/wurzel(2). Dabei fangen wir mit folgendem Initiator an:
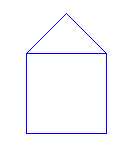
Der nächste Generator würde dann jeweils an die beiden Katheten des Dreieckes ansetzen, indem die Methode, die den obigen Initiator Zeichnet noch einmal mit der Länge laenge/wurzel(2) aufgerufen wird. Außerdem ist es wichtig zu beachten, dass die Methode immer unten-rechts beginnt zu zeichnen. Das hat zwar dann zur Folge, dass wir unter anderem die linke Kathete doppelt zeichnen, es erschien mit aber dennoch eine relativ effektive und übersichtliche Lösung.
public void pythagorasBaum(int t, double laenge, int vz) {
//Basis
if (t < 1) return;
//Unten und links
turtle.fd(laenge);
turtle.right(90);
turtle.fd(laenge);
//Schmale seite links
turtle.right(45);
turtle.fd(laenge/Math.sqrt(2));
//Rekursiv links
turtle.right(180);
pythagorasBaum(t-1, laenge/Math.sqrt(2), 1);
//Schmale Seite rechts
turtle.right(-90);
turtle.fd(laenge/Math.sqrt(2));
//Rekursiv rechts
turtle.right(180);
pythagorasBaum(t-1, laenge/Math.sqrt(2), 1);
//Rest
turtle.right(-45);
turtle.fd(laenge);
turtle.right(90);
turtle.right(90);
turtle.fd(laenge);
turtle.right(90);
turtle.fd(laenge);
turtle.right(90);
}