Neben den bekannten Sortieralgorithmen wie Insertion-Sort, Bubble-Sort und Selection-Sort, gibt es noch zahlreiche andere Algorithmen, die meist noch effektiver sind. Zu diesen zählt Merge-Sort. Dabei wird eine zu sortierende Menge an Zahlen immer weiter in der Mitte geteilt (wie bei der Binären Suche), bis nur noch zwei Werte pro Menge übrig sind. Diese können dann sortiert werden und man kann die verschiedene Mengen wieder zusammenfügen.
Quelle: https://commons.wikimedia.org/wiki/File:Merge-sort-example-300px.gif
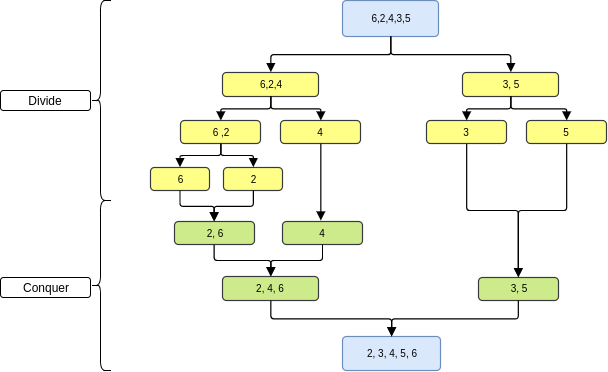Ein Beispiel für das Sortieren mit Mergesort.
public void mergesort(int links, int rechts) {
if(links < rechts){
int center = (links + rechts)/2;
mergesort(links, center);
mergesort(center+1, rechts);
merge(links,rechts);
}
}Als Basis in dem Algorithmus dient uns links = rechts. Da wir aber in diesem Fall die aktuelle Methode beenden und deshalb die Basis überflüssig ist, verwenden wir die Verzweigung if(left < right). Um nun die Menge aufzuteilen muss zuallererst eine Mitte gefunden werden center = (left + right)/2;. Wir können nun für beide Hälften die Methode rekursiv aufrufen. mergeSort(left, center); mergeSort(center+1, right);. Zu guter Letzt werden beide jeweils sortierte Hälften wieder zusammengefügt: merge(left, right);.
Die Methode merge()
Die Methode merge() ist bei diesem Sortierverfahren der eigentlich interessante Bestandteil: Sie sorgt dafür, dass wir in einem möglichst effizienten Weg zwei Sortierte Mengen wieder sortiert zusammenfügen. Man könnte zwar beispielsweise dafür auch bekannte Verfahren wie Insertionsort verwenden, dabei geht dann aber der Sinn von Mergesort und der Vorteil Mergesort zu verwenden verloren.
Das Prinzip der Methode ist wie folgt: Ich kopiere mir die erste sortierte Hälfte (wir haben ja beide Hälften in dem gleichen Array) in ein temporäres Array.
// Variablen
int center = (rechts+links)/2;
int[] tempA = new int[(center + 1)-links];
int temp = 0;
// Hälfte des Arrays wird in tempA kopiert
for(int i = links; i <= center; i++){
tempA[temp] = array[i];
temp++;
}Dann vergleiche ich den erste Wert des temp. Arrays mit dem ersten Wert der zweiten Hälfte. Sollte dieser kleiner sein, so weiß ich, dass der Wert aus dem temp. Array der kleinste Wert aus den beiden Mengen ist, weshalb ich ihn an die erste Stelle des gesamten Bereiches einsortiere. Danach vergleiche ich den zweiten Wert des temp. Arrays mit dem ersten Wert der zweiten Menge. Sollte dieses mal der Wert der zweiten Menge größer sein, so füge ich diesen Wert dem gesamten Bereich zu und gehe dann in der zweiten Menge einen Schritt weiter. Das ganze wiederhole ich so lange, bis entweder alle Werte aus dem temp. Array oder aus dem linken Bereich einsortiert wurden.
Danach kann ich die restlichen Werte, der Reihe nach an die Menge anfügen.
int i = links;
int j = center + 1;
temp = 0;
while ((i<j) && (j <= rechts)){
if(tempA[temp] <= array[j]){
//Aus dem Zwischenarray wird der Wert genommen,
//da er noch kleiner als der Wert aus der Zweiten Menge ist
array[i] = tempA[temp];
i++;
temp++;
}else{
//Der Wert aus der zweiten Menge wird genommen
array[i] = array[j];
i++;
j++;
}
}Laufzeit
MergeSort hat eine Lauzeit von $$ O(n*log(n)) $$ und ist damit schneller als die bisher behandelten Sortieralgorithmen.
Der beweis ist unter folgendem Link erreichbar: https://drive.google.com/file/d/0B8VpWNvemoCuZFJCdjBpdWxUYTQ/view?usp=sharing